Se nell’ultima puntata abbiamo giocato coi numeri, stavolta
puntiamo tutto sulla geometria, per pareggiare i conti. Ecco i due quesiti:
Il primo
Prendete un triangolo equilatero. Se non lo avete potete prendere quello che c’è qui sotto.
Adesso dividetelo in tre
pezzi tali che si possano unire per formare un rettangolo. Non è finita: con quegli stessi tre pezzi si deve poter
costruire anche un trapezio isoscele.
Il secondo
Rosa Simona, di seconda B, ha trovato questo quesito su un videogioco
e chiede a me un aiuto, così io giro a voi la domanda. Forse se ci proviamo
tutti insieme…
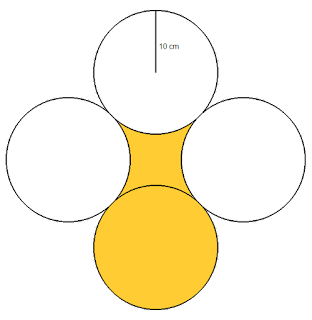
I quattro cerchi nel disegno hanno tutti uguale raggio (10 cm) e sono a due a due tangenti, cioè
si toccano in un punto. La domanda è: quanto
misura l’area della parte colorata? Spiega il ragionamento che hai fatto.
Ora, lo so che in prima non abbiamo ancora affrontato il
calcolo delle aree. So anche che nemmeno in seconda abbiamo ancora parlato del
cerchio. Il bello è proprio qui: non serve saper calcolare l’area del cerchio
(e questo è un primo suggerimento). E sono sicuro che quel poco che qui serve
sapere sulle aree lo sapete già dalla scuola primaria. Certo, per trovare la
soluzione ognuno ci deve mettere qualcosa di proprio (e questo è un
secondo suggerimento).
Una piccola nota, per essere onesti e un po’ pignoli (potete
anche non leggerla, se preferite): se per qualche caso passasse di qui un
matematico vero, probabilmente avrebbe
qualcosa da ridire (ad esempio: “Bisognerebbe
dimostrare che questo è adiacente a quello, che quell’angolo è proprio un
angolo di quel tipo…” cose così). Forse però, per questa volta, possiamo
sorvolare su certi dettagli.
Ci sentiamo venerdì prossimo per le soluzioni.


3 commenti:
Molto carini.
Evviva la geometria, seppure: sarà mica geometria?? :-)
Ragazzi (più che altro per i miei), se dovessero apparirvi complessi, badate che abbiamo lavorato più di una volta su problemi-giochi simili.
Le dimostrazioni, concordo, per il momento si può sorvolare. Seppure, per il primo quesito, da quelli della terza si potrebbero pretendere ... :-)
grazie,
buona domenica ... per noi adulti elettorale?! :-)
g
Perfettamente d'accordo sulle dimostrazioni. Forse potremmo dire che più le spiegazioni sono precise meglio è. Che non sarà proprio una richiesta di dimostrazione ma, insomma.
Per quanto riguarda le elezioni dirò che stamattina ci siamo svegliati in un mondo bianco e freddo. Non è un'affermazione sulla politica italiana, è proprio che nevica. Per il momento io non esco di casa :-)
Comunque si può votare anche domani. E aggiungo che, siccome la nostra scuola è sede di seggio, siamo a casa anche martedì.
Il lato buono delle elezioni :-D
Aah, ingiustizie!! Da noi i seggi elettorali sempre nell'edificio della primaria! :-))
Anche noi ci siamo svegliati con la neve e nevica tuttora. Perciò ho messo anche il punto interrogativo.. perché neppure io esco di casa :-)
Concordo su quello che precisi quanto alle dimostrazioni. Non chiamiamole dimostrazioni ma spieghiamo bene i *perché* !
g
Posta un commento