Se cercate risposte, siete nel posto giusto.
Se invece cercate le domande, dovete andare a guardare il post
Due a settimana..._17 della
prof Giovanna. Perchè qui tentiamo di dare le nostre risposte a
quelle domande.
Se invece cercate la risposta alla domanda fondamentale sulla vita, l'universo e tutto quanto... ripassate di qui tra qualche giorno: ne parleremo nella prossima puntata di Sarà mica matematica!
Ma non divaghiamo. Stavamo dicendo: i quesiti di Due a settimana..._17.
QUESITO 1
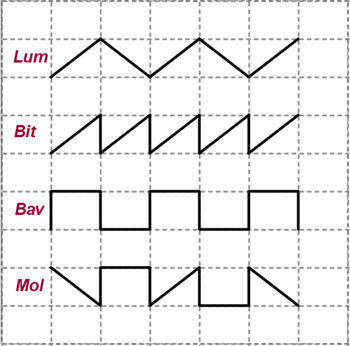
Questa l'immagine pubblicata dalla prof.
Il libro di scuola le chiamerebbe linee spezzate aperte. E invece no, sono
tracce di bava di lumaca su un pavimento di piastrelle rettangolari! Data la lunghezza delle tracce di Lum, Bit e Bav, si vuole sapere quanto lunga è la traccia di Mol.
Vediamo le nostre soluzioni, in rigoroso ordine sparso (ma dando la precedenza a chi ha scritto via mail).
Serena G scrive:
Io ho calcolato che se la traccia di Lum è lunga 25 decimetri ogni tratto è lungo 5 decimetri, perché 25:5 fa 5.
La lunghezza della traccia di Bit è 37 decimetri, perciò se sottraggo 25 (somma delle diagonali) il risultato è 12. Per calcolare le parti corte del rettangolo, divido 12 per 4= 3 decimetri.
Nella traccia di Bav sottraggo i lati corti che misurano in tutto 18 decimetri (6 x 3).
Per trovare i lati lunghi faccio 38 – 18 = 20 e poi lo divido per 5 ( lati lunghi ) = 4 decimetri.
La traccia di Mol è formata da: 3 diagonali, 4 lati corti e 2 lati lunghi, perciò in totale misura 35 decimetri (3 x 5 + 4 x 3 + 2 x 4).
È quello che dice anche Edoardo O:
Innanzitutto devo dividere la lunghezza di Lum per il numero di segmenti su ogni piastrella:
25:5=5 decimetri.
Poi per trovare il valore dei segmenti perpendicolari di Bit devo togliere la lunghezza di Lum a Bit, così da lasciare solo i segmenti perpendicolari:
37-25=12 decimetri 12:4=3 decimetri
Per trovare i segmenti orizzontali di Bav devo togliere dalla sua misura il valore dei segmenti verticali:
38-(3x6)=38-18=20 decimetri 20:5=4 decimetri
Quindi Mol misurerà:
(5x3)+(3x4)+(2x4)=15+12+8=35 decimetri.
Potrei copiare e incollare le parole di diverse altre persone ma sarebbe un po' troppo noioso: nella sostanza tutti hanno seguito lo stesso filo di ragionamenti. Mi limito a citare i solutori e spero non si offendano se non vedono pubblicati i loro scritti
.
Alberto C, Naomi R e Stefano P hanno inviato soluzioni via mail.
Hanno preferito la versione cartacea:
Alice D, Ivan Z, Gaia B, Giorgia M, Pietro B, Simone S, Matilde e Paolo D.
Qualcuno (parecchi!) ha seguito il procedimento corretto ma ha sbagliato qualche calcolo. Sono tentato di menzionare anche loro ma mi trattengo: qualche errore di calcolo è comprensibile in una verifica, con un po' di tensione in corpo e il tempo che stringe. Qui lo è molto meno.
QUESITO 2
Qui le strade per arrivare alla soluzione erano parecchie e ognuno ha seguito la propria, come è bene che sia.
Sara C allega una figura in cui mostra che la elle si può suddividere in sette quadratini di lato 2.
Da qui la soluzione è facile: ogni quadratino ha area (2 cm)2 = 4 cm2
Sette quadratini significa 7 x 4 cm2 = 28 cm2
Sara in realtà fa un uso delle unità di misura così sconsiderato che mi metterei le mani nei capelli se solo li avessi ancora! Allora sistemo le cose e glisso con signorilità.
Hanno seguito lo stesso ragionamento anche
Nelson R e
Edoardo O.
Simone S e Naomi R, ciascuno per conto suo, hanno percorso la strada dei sette quadratini ma anche un'altra, che potremmo chiamare "
dei due rettangoli e un quadratino".
Eccola, nelle parole di
Stefano P, il quale manda questa figura
e commenta:
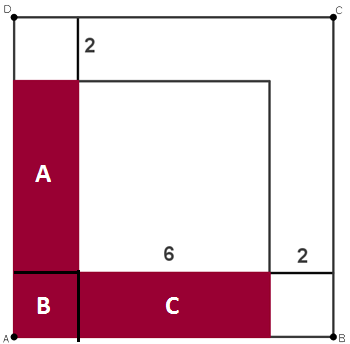
per calcolare l'area della L in rosso posso:
- dividerla in 3 parti (2 rettangoli da 6cm x 2cm indicati A e C nella figura e un quadratino da 2cm x 2cm indicato con B),
- calcolare le aree delle 3 figure (6cm x 2cm = 12cm2; 6cm x 2cm = 12cm2; 2cm x 2cm = 4cm2)
- infine sommarle facendo 12cm2 + 12cm2 + 4cm2 = 28cm2.
Hanno scoperto la soluzione
"
dei due rettangoli e un quadratino" anche
Nicole M e Pietro B.
Mattia C non allega alcuna immagine alla sua mail ma scrive con sufficiente chiarezza:
Per calcolare l'area della elle colorata bisogna prima calcolare l'area totale del quadrato ABCD, poi quella dei quadrati più piccoli, sommarle e poi sottrarre l'area dei quadrati più piccoli da quella del quadrato più grande; quindi il risultato deve essere diviso per due per ottenere l'area di una singola elle.
Il risultato è: 28 cm2
Se sorvoliamo sul fatto che l'unità di misura è una mia aggiunta, è una buona soluzione. (Ma quanto sarebbe stata più chiara se accompagnata da una buona figura!)
Anche
Giorgia M l'ha trovata. Purtroppo considera il lato del quadratone lungo 8 cm anziché 10 cm come dovrebbe.
Alberto C manda una mail senza immagini (
aaargh!!) e cerca di spiegarsi a parole. Io copio, incollo e metto un po' in ordine:
Ho diviso la L in due rettangoli, uno più grande e l'altro più piccolo. Il più grande ha la base di 8 cm2 e l'altezza di 2 cm2; facendo base per altezza fa 16 cm2. Nel'altro la base è 2 cm e l'altezza 6 cm; facendo base per altezza risulta 12 cm2.
Se sommo 16 cm2 e 12 cm2 ottengo un'area totale di 28 cm2.
Hanno individuato scelto la soluzione "
dei due rettangoli" anche
Ivan Z, Gaia B, Giulia DM, Leonardo R e Moris N.
Di possibilità ce ne sono senz'altro parecchie ancora. Ad esempio, nessuno ha pensato alla soluzione che a me piace di più
:
Il quadrato AIGL ha lato lungo 8 cm pertanto ha area 64 cm
Il quadrato EFGH ha lato 6 cm, quindi la sua area è 36 cm.
L'area della L rossa è AAIGL – AEFGH = 64 cm2 - 36 cm2 = 28cm2.
QUESITO 3
Tutti hanno stampato la figura originale, oppure l'hanno ridisegnata a mano, seguendo le indicazioni. A quanto capisco, solo
Serena G, di prima B, ha tentato di ricostruire la figura di partenza con Geogebra, come avevamo discusso in classe. Questa è la sua opera.
La pubblico per rendere merito a Serena, che ci ha provato con impegno! A prima vista la figura sembra quasi identica all'originale della prof Giovanna. Ma uno sguardo appena più attento nota alcune irregolarità (soprattutto nel quadrato centrale), segno che la costruzione con Geogebra non è corretta. Vale la pena di riparlarne meglio in classe.
Torniamo al quesito.
Si trattava di smontare la figura di partenza e riorganizzare i pezzi per costruire queste sagome (che sono quindi equiscomponibili rispetto al quadrato originale)
Qualcuno ha cercato di rispondere solo a parole.
Edoardo O, ad esempio, scrive:
Per ottenere la “T” bisogna prendere la figura n4, la n2 e la n6 e unirle per comporre la parte orizzontale, per ottenere la parte verticale devo prendere la figura n1 e la n5 e le devo affiancare alla n3, che resta invariata.
Per ottenere la “Freccia” devo prendere la figura 1 e 5 come sono già nel disegno e capovolgerli insieme, poi prendo la figura n3 e la ruoto di 180°: le affianco in modo da ottenere la “punta” della freccia. Poi, per trovare il “busto” devo affiancare la figura n2 alla n4 e unirle alla figura n6.
Per ottenere la “Croce” devo prendere le figure n5, n1 e n3 e formare la parte verticale (come fatto in precedenza). Per formare la parte orizzontale devo prendere le figure n6, n4 e n2.Unendo la parte n4 e la n2 ottengo due quadrati che vado a sovrapporre in mezzo alla parte verticale.
Apprezzo la fiducia nelle potenzialità della lingua italiana ma in questo caso era proprio meglio ricorrere alle immagini: più veloce e più chiaro.
Per quanto Edoardo si esprima con chiarezza, mi ci è voluto un po' per capire che non costruisce una
croce greca, con tutti i bracci uguali (così era la figura richiesta) ma una
croce latina con un braccio più lungo degli altri.
I sei poligoni, in effetti,
si possono comporre in parecchi modi. Alcuni sembrano giusti ma non lo sono: le proporzioni delle figure non corrispondono a quelle richieste dal quesito. I due bracci della T, ad esempio, devono essere di uguale lunghezza.
Le combinazioni corrette sono più di una. Ma tutte sono variazioni sullo stesso tema.
Sfrutterò le immagini più accurate che sono arrivate via mail per rendere l'idea delle possibili soluzioni. Si tratta delle foto fatte da Stefano P e da Naomi R. Ho rimaneggiato entrambe solo un poco, per togliere lo sfondo.
 |
| Le composizioni di Stefano P |
 |
| Le composizioni di Naomi R |
Hanno costruito, ognuno a proprio modo, le tre figure:
Giorgia M (la quale disegna le figure e spiega anche a parole, molto bene!),
Leonardo R e
Sara C. Sembra esserci riuscito anche Mattia C ma dalla sua descrizione, solo a parole, non riesco ad stabilirlo con certezza.
Hanno costruito due figure:
Alberto C (T e freccia),
Pietro B (T e freccia) e
Simone S (freccia e croce).
Sono riusciti a costruire solo una figura:
Alice D (la croce),
Gaia B, (la T),
Giulia DM (la T) e
Ivan Z (la freccia).
Credo di aver detto tutto. Credo. Chi si accorgesse che ho dimenticato qualcuno o qualcosa batta un colpo!
Resta da ringraziare ancora una volta la
prof Giovanna e resta da dare a tutti l'appuntamento per nuovi giochi: la prossima puntata di Sarà mica matematica sarà
a tema. Più di un tema, per essere più precisi.
Volete sapere
quali temi? Niente di più facile:
vi basta passare di qui tra qualche giorno.