Sarà mica matematica 29, le soluzioni

Aprile, maggio. È tempo di vacanze pasquali, ponti, ponticelli, gite scolastiche.
Poteva il post con le soluzioni essere puntuale? Si poteva evitare il ritardo?
Risposta esatta! Dunque, col passo un po' strascicato tipico dell'ultimo mese di scuola (ma è una mia impressione o quest'anno i piedi sembrano più pesanti del solito?) ci apprestiamo a chiudere l'ultimo Sarà mica mate di quest'anno (scolastico, s'intende). Vediamo le nostre risposte ai due quesiti pubblicati qui.

Il primo

Comincio con la doverosa citazione (e annesso ringaziamento) del blog da cui ho preso spunto, Dropsea. Questo il post con il gioco originale.
Io ho deciso di riproporlo con un numero di partenza (o forse di arrivo) più grande. In questo modo aumentano le possibili soluzioni e il gioco diventa più semplice (o almeno questa era la mia intenzione). Quanto alle soluzioni diverse, direi che l'obiettivo è raggiunto. Forse perfino troppo. La maggioranza ha risposto via biglietto cartaceo che io, in mancanza di uno scanner, ho fotografato. In alcuni casi la foto è riuscita male e sono stato costretto a ricostruire a computer il reticolo.
Allora cominciamo con i reticoli proposti da Sophia Z., che spedisce un paio di pdf che posso riusare così come sono. Trova quattro soluzioni, due hanno 9 come numero minore. La prima di queste  è stata trovata anche da Sarah T.

 

Altre due partono con il 6.

 

Nella parole di Sophia:
-Osservo che i più piccoli numeri primi divisori di 540 sono 2, 3 e 5 (sono anche gli unici, aggiungo io), quindi:

540 ÷ 2 = 270           540 ÷ 3 = 180           540 ÷ 5 = 108

-Noto che solo 270 e 180 sono divisibili per 2, per 3 e per 5, mentre 108 è divisibile solo per 2 e per 3, quindi lo posiziono dove ci sono solamente 2 legami.
-Proseguendo, osservo che alcuni numeri devono avere per forza un divisore comune, quindi devo calcolare il Massimo Comune Divisore.
-Infine noto che (nella prima soluzione) il numero 5 si trova solamente sulle frecce orizzontali, il numero 2 solo su quelle verticali e il numero 3 solo su quelle oblique.
-Quindi, per le altre soluzioni occorre solamente dividere per 2, per 3 o per 5 il numero considerato, facendo, però, attenzione al senso delle frecce (orizzontale, verticale o obliquo).
Era possibile partire anche con il numero 3, come dimostrano le due soluzioni qui sotto, una proposta da Davide C. (di seconda B), l'altra da Sharon C..

Andrea G. ne ha trovata una che come numero più piccolo ha il 2...

Andrea ha seguito un procedimento simile a quello usato da Sophia: ha scomposto 540 in fattori primi, poi lo ha diviso per 2, per 3 e per 5, ottenendendo 270, 180 e 108. Poi ha proseguito di volta in volta cercando il divisore più grande possibile... cioè il MCD. Ad esempio MCD (270; 180) = 90.
MOLTO BENE!

Ancora Andrea propone un'altra soluzione (senza spiegazione, stavolta), che invece parte dal numero 1

Usare il numero 1, era un po' come giocare il jolly. Non è un caso se le soluzioni di questo tipo - senz'altro valide ma un po' meno "pregiate", per così dire - siano state le più numerose .

Ad esempio c'è la seguente possibilità, scoperta da Alice A., Lorenzo B. e Nicolò A. di prima B

Oppure c'è quest'altra, trovata da Aman A. e da Damanjot S.

Oppure quella di Alessandro N., il quale, dopo aver individuato i divisori 1, 2, 3 e 5 (non dichiara perché abbia scelto proprio questi ma di sicuro vanno bene) dice: partendo da sotto ho messo i numeri più piccoli e poi salendo ho moltiplicato sempre per i divisori principali di 540.

 

Stefano S., invece segue la stessa strada al contrario: nota che 540 è divisibile per 2, 3 e 5, poi "scende" dividendo secondo i vari criteri di divisibilità.

Oppure ancora, quella di Davide C. (prima B)

Infine quelle di Cristian C., che ne propone ben tre.

 

Il secondo

Si è rivelato ben più ostico. Hanno risolto solo Amanda P., Davide C. e Sophia Z., tutti di seconda B. Il percorso seguito è lo stesso per tutti e tre. Amanda e Davide hanno consegnato la loro risposta su foglio di carta, Sophia via mail. Siccome sono notoriamente pigro e scansafatiche, sfrutto la figura e le parole di Sophia, che posso copincollare (il neologismo è bruttino ma ormai è entrato nei vocabolari italiani, insieme a forwardare, debuggare, restartare, googlare...).

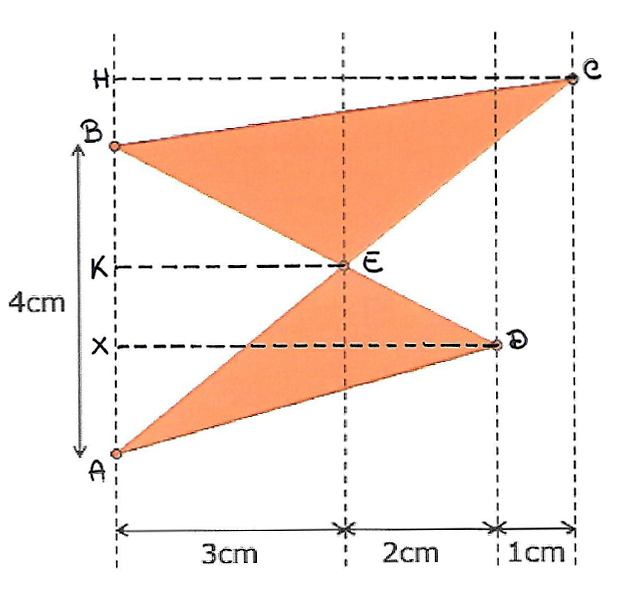
Assegnando le lettere ai vertici di tutti i triangoli che compaiono nella figura, osservo che l'area del triangolo BCE è data dalla differenza tra l'area del triangolo ABC e quella del triangolo ABE. Analogamente noto che l'area del triangolo AED è data dalla sottrazione dell'area del triangolo ABE a quella del triangolo ABD. 
Per calcolare le aree dei triangoli, traccio le tre altezze CH, EK e DX.
 
 Per trovare la misura della superficie del triangolo ABC devo eseguire:

A_ABC = AB × CH ÷ 2 = 4 × 6 ÷ 2 = 12.

Per ottenere l'area del triangolo ABE devo calcolare: 

A_ABE = AB × EK ÷ 2 = 4 × 3 ÷ 2 = 6. 

.

Ora manca solamente l'area del triangolo ABD: 

A_ABD = AB × DX ÷ 2 = 4 × 5 ÷ 2 = 10.

L'area del triangolo BCE si ottiene eseguendo: 

A_BCE = A_ABC - A_ABE = 12 - 6 = 6.

Mentre quella del triangolo AED: 

A_AED = A_ABD - A_ABE = 10 - 6 = 4.

Infine, per calcolare l'area totale della figura colorata, devo eseguire la somma delle due aree trovate precedentemente:

A = A_BCE + A_AED = 6 + 4 = 10.

Personalmente ci aggiungerei quanche unità di misura, ma insomma, mi complimento con i tre solutori.

Per la verità sono arrivate anche un paio di altre soluzioni alternative. Sono anche apprezzabili ma piuttosto complicate e soprattutto contengono passaggi che vanno oltre il livello "scuola media". Spero che gli interessati non se ne abbiano a male se non le pubblico causa eccesso di aiuto.

Sono ragionevolmente sicuro di dimenticare qualcuno. Nel caso, i dimenticati battano un colpo.

Così siamo alla fine. Non solo di questa puntata: Sarà mica matematica chiude i battenti e appende in vetrina il cartello

CHIUSO PER FERIE (si fa per dire...),

RIAPRIREMO... PRESTO,

forse anche prima.