Ce l'ho fatta!
Ho corretto tutte le risposte ai quesiti che la prof Giovanna ci aveva proposto in Due a settimana..._19.
Non è che fossero poi tante risposte, è che io ero in troppi altri impegni impegnato.
Ma ce l'ho fatta, mi faccio i complimenti.
Si parte? Si parte!
IL PRIMO
Cominciamo con la risposta di Andrea G (di prima B):
A+B+A=BC
B+C=B quindi C=0
A+B+A=B0
La somma di tre numeri ad una cifra è inferiore a 30.
Quindi B0 potrà essere il numero 10 oppure il numero 20.
Quindi B potrebbe essere 1 oppure 2.
Se B fosse 1 allora A+1+A=10 quindi A+A=10-1=9 quindi non possibile perché 9 non è divisibile per due.
Allora B=2, difatti A+2+A=20 quindi A+A=20-2=18 quindi A=18:2=9.
La cifra che corrisponde alla lettera A è 9.
Tutti gli altri hanno scelto la strada lunga.
Le risposte sono tutte simili, ne faccio una sintesi sfruttando principalmente le frasi di Edoardo O. Userò anche la figura di Nicole M, perché il colore del tetto mi piace, ecco.
Per la seconda B: Alberto C, Alessia P, Alice D, il solito Anonimo (sempre ammesso che sia di seconda!), Edoardo&Christian, Giorgia M, Ivan Z, Martina D, Matilde & Paolo D, Nelson R, Nicole M, Nihad K,
Per la terza B: Pietro B, Riccardo R. Naomi R fa tutto per bene ma alla fine calcola il perimetro anziché l'area.
Ho corretto tutte le risposte ai quesiti che la prof Giovanna ci aveva proposto in Due a settimana..._19.
Non è che fossero poi tante risposte, è che io ero in troppi altri impegni impegnato.
Ma ce l'ho fatta, mi faccio i complimenti.
Si parte? Si parte!
IL PRIMO
Cominciamo con la risposta di Andrea G (di prima B):
A+B+A=BC
B+C=B quindi C=0
A+B+A=B0
La somma di tre numeri ad una cifra è inferiore a 30.
Quindi B0 potrà essere il numero 10 oppure il numero 20.
Quindi B potrebbe essere 1 oppure 2.
Se B fosse 1 allora A+1+A=10 quindi A+A=10-1=9 quindi non possibile perché 9 non è divisibile per due.
Allora B=2, difatti A+2+A=20 quindi A+A=20-2=18 quindi A=18:2=9.
La cifra che corrisponde alla lettera A è 9.
Stefano P, di terza B, ragiona in modo molto simile:
Se sommando le cifre di bc ottengo b vuol dire che c vale 0 perché b + 0 = b.
Per sapere quanto vale la lettera a posso prima scoprire quanto vale la b.
Se bc è un numero di due cifre che finisce per 0 ed è il risultato della somma di tre cifre, allora non può essere 10, perché l'unico modo per fare 10 con dei numeri naturali positivi è 3 + 4 + 3 (a + b + a), ma la b non viene 1 quindi non è giusto.
Il numero massimo che si può fare sommando tre cifre è 27, quindi escludendo 10, bc deve essere per forza 20.
Per fare 20 con aba ho trovato la combinazione 929. Dunque la cifra rappresentata dalla lettera a è 9.
Naomi R, anche lei di terza B, sceglie una strada luunga! Dichiara innanzitutto la soluzione, poi spiega. Confesso che ci ho messo un po' a capire, poi sono stato tentato di modificare per rendere più chiaro, poi ho preferito sopravvivere e lascio ai lettori l'onere (e onore, certo) della comprensione.
:-D
A=9 B=2 C=0
2 B 2; B= 6 (10); 7(11); 8(12); 9(13)
3 B 3; B= 4 (10); 5(11); 6(12); 7(13); 8(14); 9(15)
4 B 4; B= 2 (10); 3(11); 4(12); 5(13); 6(14); 7(15); 8(16); 9(17)
5 B 5; B= 0 (10);1(11); 2(12); 3(13); 4(14); 5(15); 6(16); 7(17); 8(18); 9(19)
6 B 6; B= 0 (12);1(13); 2(14); 3(15); 4(16); 5(17); 6(18); 7(19); 8(20); 9(21)
8 B 8; B= 0 (16);1(17); 2(18); 3(19); 4(20); 5(21); 6(22); 7(23); 8(24); 9(25)
9 B 9; ?= 0 (18);1(19); 2(20); 3(21); 4(22); 5(23); 6(24); 7(25); 8(26); 9(27)
Poi elimino tutti i numeri che non hanno la cifra sommata delle B uguale alla prima cifra del risultato, ottenuto sommando A+B+A. rimangono quindi:
5 B 5; B= 1(11)
6 B 6; B=1(13)
8 B 8; B=1(17)
9 B 9; B= 1(19); 2(20)
Infine,l’unico numero che ha come cifra finale 0 è 20 quindi:
A+B+A=B+C 9+2+9=20
B+C=B 2+0=2
Rachele C, di prima B, un po' ragiona, un po'... no :-):
Per trovare le lettere a, b, c sono partita cercando la lettera b.
Dato che sommando le cifre di bc ottengo il numero di una cifra b, sono sicura che la lettera c sia uguale a zero: b + c = b quindi c = 0
A questo punto b potrebbe essere un numero da 1 a 9.
Sono andata a tentativi e ho capito che b può essere uguale solo a 2. Ma non è chiaro perché (NdP, ovvero Nota del Prof).
b=2 bc=20
Poi so che a+b+a=bc
Quindi bc-b=2a 20-2=18
Quindi a=18:2=9
Mi piace in particolare la penultima frase, che mostra una certa abilità algebrica. Conto che Rachele la tiri fuori quando arriveremo al calcolo letterale e alle equazioni!
Giada A, di prima B, è molto simpatica e un pizzico confusionaria: manda una mail con una risposta, poi ne manda un'altra, con oggetto "HO SBAGLIATOOO", in cui sostiene di aver scritto una "cavolata assurda". Leggo entrambe le mail e mi pare siano uguali nella sostanza. Però obbedisco a Giada che mi intima: NON GUARDI QUELLA PRIMA, è SBAGLIATISSIMA. Copio e incollo il testo della seconda mail:
ABC può essere diversi numeri : 920, 926,925,924,923... per trovare A ho pensato il numero più vicino al 10 che è 9 poi, per trovare BC, ho messo tutti i numeri sotto il 9 che sommati venivano B.Se sommando le cifre di bc ottengo b vuol dire che c vale 0 perché b + 0 = b.
Per sapere quanto vale la lettera a posso prima scoprire quanto vale la b.
Se bc è un numero di due cifre che finisce per 0 ed è il risultato della somma di tre cifre, allora non può essere 10, perché l'unico modo per fare 10 con dei numeri naturali positivi è 3 + 4 + 3 (a + b + a), ma la b non viene 1 quindi non è giusto.
Il numero massimo che si può fare sommando tre cifre è 27, quindi escludendo 10, bc deve essere per forza 20.
Per fare 20 con aba ho trovato la combinazione 929. Dunque la cifra rappresentata dalla lettera a è 9.
Naomi R, anche lei di terza B, sceglie una strada luunga! Dichiara innanzitutto la soluzione, poi spiega. Confesso che ci ho messo un po' a capire, poi sono stato tentato di modificare per rendere più chiaro, poi ho preferito sopravvivere e lascio ai lettori l'onere (e onore, certo) della comprensione.
:-D
A=9 B=2 C=0
Innanzitutto, per far sì che B+C=B, C deve avere un valore neutro, quindi 0.
Sapendo che la somma A+B+A dà come risultato BC e supponendo che A abbia un valore compreso tra 1 e 9 e che B abbia un valore tra 0 e 9 (perché A non possa valere 0 non è dichiarato ma si può intuire: i numeri non cominciano con la cifra 0), sommo A a B facendo in modo che la somma dia un numero di due cifre (tra parentesi ho riportato il risultato che si ottiene sommando a un certo valore di A un certo valore di B):
1 B 1; B= 8 (10); 9(11)Sapendo che la somma A+B+A dà come risultato BC e supponendo che A abbia un valore compreso tra 1 e 9 e che B abbia un valore tra 0 e 9 (perché A non possa valere 0 non è dichiarato ma si può intuire: i numeri non cominciano con la cifra 0), sommo A a B facendo in modo che la somma dia un numero di due cifre (tra parentesi ho riportato il risultato che si ottiene sommando a un certo valore di A un certo valore di B):
2 B 2; B= 6 (10); 7(11); 8(12); 9(13)
3 B 3; B= 4 (10); 5(11); 6(12); 7(13); 8(14); 9(15)
4 B 4; B= 2 (10); 3(11); 4(12); 5(13); 6(14); 7(15); 8(16); 9(17)
5 B 5; B= 0 (10);1(11); 2(12); 3(13); 4(14); 5(15); 6(16); 7(17); 8(18); 9(19)
6 B 6; B= 0 (12);1(13); 2(14); 3(15); 4(16); 5(17); 6(18); 7(19); 8(20); 9(21)
8 B 8; B= 0 (16);1(17); 2(18); 3(19); 4(20); 5(21); 6(22); 7(23); 8(24); 9(25)
9 B 9; ?= 0 (18);1(19); 2(20); 3(21); 4(22); 5(23); 6(24); 7(25); 8(26); 9(27)
Poi elimino tutti i numeri che non hanno la cifra sommata delle B uguale alla prima cifra del risultato, ottenuto sommando A+B+A. rimangono quindi:
5 B 5; B= 1(11)
6 B 6; B=1(13)
8 B 8; B=1(17)
9 B 9; B= 1(19); 2(20)
Infine,l’unico numero che ha come cifra finale 0 è 20 quindi:
A+B+A=B+C 9+2+9=20
B+C=B 2+0=2
Rachele C, di prima B, un po' ragiona, un po'... no :-):
Per trovare le lettere a, b, c sono partita cercando la lettera b.
Dato che sommando le cifre di bc ottengo il numero di una cifra b, sono sicura che la lettera c sia uguale a zero: b + c = b quindi c = 0
A questo punto b potrebbe essere un numero da 1 a 9.
Sono andata a tentativi e ho capito che b può essere uguale solo a 2. Ma non è chiaro perché (NdP, ovvero Nota del Prof).
b=2 bc=20
Poi so che a+b+a=bc
Quindi bc-b=2a 20-2=18
Quindi a=18:2=9
Mi piace in particolare la penultima frase, che mostra una certa abilità algebrica. Conto che Rachele la tiri fuori quando arriveremo al calcolo letterale e alle equazioni!
Nicole M, di seconda B procede per tentativi, che è pur sempre una possibilità. Scrive: la risposta che trovo è 929, dopo una serie di tentativi applicando la stessa logica è l’unico che rispetta le regole.
Su carta, rispondono (più o meno) correttamente ma in maniera secca, senza spiegazioni esaurienti: Alberto C, Alice D (per tentativi), Christian&Edoardo (per tentativi), Emma C, Giorgia M, Iman B, Lorenzo Z, Matilde & Paolo D, Noemi N.
Raccontano un po' di più: Simone S (un po' di ragionamento e un po' di tentativi), il solito Anonimo (spiega il procedimento in 3 passi ma non è che siano chiarissime tutte le ragioni di tali passi), Riccardo R, Pietro B (giustifica il primo passo, ma non il seguito).
IL SECONDO
Si è rivelato un avversario ostico. Molti ci hanno rinunciato in partenza e molti sono caduti provando. Ma è cadendo e rialzandosi che si impara a camminare...
Si partiva da questa figura e si chiedeva la misura del contorno a tratto spesso.
La risposta di Stefano P (terza B): se sommo i perimetri del rettangolo grande più quello dei tre piccoli, devo togliere dal totale le linee sottili non evidenziate.
Se guardo il rettangolo con centro in A, le righe sottili sono il suo semi perimetro, perché sono lunghe come due suoi mezzi lati corti e due suoi mezzi lati lunghi. Le linee sottili sono quindi la metà del perimetro del rettangolo piccolo.
Questo ragionamento lo applico anche agli altri due rettangolini.
Dalla somma dei perimetri devo togliere quindi metà del perimetro dei rettangoli piccoli: 30cm + (20cm : 2) = 40cm.
Andrea G (prima B): per trovare quanti centimetri è lungo il contorno disegnato a tratto spesso bisogna prima trovare quanto è la somma dei lati disegnati con tratti fini.
La somma dei lati con tratti fini è uguale alla somma dei perimetri dei tre triangoli piccoli diviso per due, quindi = 20:2=10 cm. [Non è chiaro perché, una spiegazione ci sarebbe stata bene]
La parte disegnata con tratti fini del rettangolo grande è lunga la metà della somma dei lati dei tre mini rettangoli con tratti fini, quindi è 10:2=5 cm.
Quindi la lunghezza della parte con tratti spessi del rettangolo grande è uguale a 30-5=25 cm.
La lunghezza dei lati disegnati con tratto spesso dei tre rettangoli piccoli è uguale a 20-5= 15 cm.
Quindi tutto il contorno disegnato con tratti fini è uguale a 25+15=40 cm.
2pABCD=30cm
Tra chi ha scelto di consegnare su carta ha risposto bene Anonimo (sempre lui, o forse lei, chissà), Noemi N (spiegazione da migliorare ma il ragionamento c'è), Pietro B, Riccardo R, Simone S.
IL TERZO
I primini erano esentati da questa fatica: serve il teorema di Pitagora e loro non lo conoscono ancora, come è normale che sia. Invece ne abbiamo già piuccheparlato in terza e in seconda.
Si è rivelato un avversario ostico. Molti ci hanno rinunciato in partenza e molti sono caduti provando. Ma è cadendo e rialzandosi che si impara a camminare...
Si partiva da questa figura e si chiedeva la misura del contorno a tratto spesso.
La risposta di Stefano P (terza B): se sommo i perimetri del rettangolo grande più quello dei tre piccoli, devo togliere dal totale le linee sottili non evidenziate.
Se guardo il rettangolo con centro in A, le righe sottili sono il suo semi perimetro, perché sono lunghe come due suoi mezzi lati corti e due suoi mezzi lati lunghi. Le linee sottili sono quindi la metà del perimetro del rettangolo piccolo.
Questo ragionamento lo applico anche agli altri due rettangolini.
Dalla somma dei perimetri devo togliere quindi metà del perimetro dei rettangoli piccoli: 30cm + (20cm : 2) = 40cm.
Andrea G (prima B): per trovare quanti centimetri è lungo il contorno disegnato a tratto spesso bisogna prima trovare quanto è la somma dei lati disegnati con tratti fini.
La somma dei lati con tratti fini è uguale alla somma dei perimetri dei tre triangoli piccoli diviso per due, quindi = 20:2=10 cm. [Non è chiaro perché, una spiegazione ci sarebbe stata bene]
La parte disegnata con tratti fini del rettangolo grande è lunga la metà della somma dei lati dei tre mini rettangoli con tratti fini, quindi è 10:2=5 cm.
Quindi la lunghezza della parte con tratti spessi del rettangolo grande è uguale a 30-5=25 cm.
La lunghezza dei lati disegnati con tratto spesso dei tre rettangoli piccoli è uguale a 20-5= 15 cm.
Quindi tutto il contorno disegnato con tratti fini è uguale a 25+15=40 cm.
Edoardo O (seconda B):
Per trovare il perimetro del tratto rosso marcato:
-devo togliere dal perimetro dei rettangoli annessi al rettangolo grande ¼ [anche qui: una piccola spiegazione avrebbe giovato.]
- ¼ x 20cm= 5cm
-devo togliere dal perimetro dei rettangoli annessi al rettangolo grande ¼ [anche qui: una piccola spiegazione avrebbe giovato.]
- ¼ x 20cm= 5cm
- 20cm-5cm=15cm
-devo togliere la stessa misura dal perimetro del rettangolo grande
- 30cm-5cm=25cm
-adesso devo sommare: 25cm+15cm=40cm.
-devo togliere la stessa misura dal perimetro del rettangolo grande
- 30cm-5cm=25cm
-adesso devo sommare: 25cm+15cm=40cm.
Naomi R (terza B) allega un'immagine (e stavolta rinuncio a togliere lo sfondo bianco ma solo per questioni di tempo)
E spiega:
2pABCD=30cm
2ptot rettangolini=20cm
20cm= 2a+2b+2c+2d+2e+2f => 20cm=2(a+b+c+d+e+f) => 20cm x 1/2 = a+b+c+d+e+f => a+b+c+d+e+f=10cm
AX è uguale alla metà di a e XK è uguale alla metà di b e applicando questo ragionamento anche per gli altri due rettangolini, ottengo che:
2ptotale= 30cm + (a+b+a/2+b/2-a/2-b/2)+(c+d+c/2+d/2-c/2-d/2)+(e+f+e/2+f/2-e/2-f/2)= 30cm +(a+b+c+d+e+f).
20cm= 2a+2b+2c+2d+2e+2f => 20cm=2(a+b+c+d+e+f) => 20cm x 1/2 = a+b+c+d+e+f => a+b+c+d+e+f=10cm
AX è uguale alla metà di a e XK è uguale alla metà di b e applicando questo ragionamento anche per gli altri due rettangolini, ottengo che:
2ptotale= 30cm + (a+b+a/2+b/2-a/2-b/2)+(c+d+c/2+d/2-c/2-d/2)+(e+f+e/2+f/2-e/2-f/2)= 30cm +(a+b+c+d+e+f).
Quindi, poiché a+b+c+d+e+f=10 cm, =>2ptotale= 30cm +10cm = 40cm
Tra chi ha scelto di consegnare su carta ha risposto bene Anonimo (sempre lui, o forse lei, chissà), Noemi N (spiegazione da migliorare ma il ragionamento c'è), Pietro B, Riccardo R, Simone S.
I primini erano esentati da questa fatica: serve il teorema di Pitagora e loro non lo conoscono ancora, come è normale che sia. Invece ne abbiamo già piuccheparlato in terza e in seconda.
Questo è un classico quesito da prova Invalsi, ci offre l'occasione per allenarci ma anche per guardare un po' più da vicino quello strano mostro che chiamano "L'Invalsi".
Potremmo discutere a lungo sul valore di quelle prove ma non lo faremo. Magari un'altra volta. Resta il fatto che la prova Invalsi è una realtà: bella o brutta, ci tocca. Facciamola al meglio, io dico.
Uno degli aspetti da considerare è il tempo. Alcune risposte si possono trovare in trenta secondi oppure in cinque minuti. La prima alternativa è meglio, in genere. Seguire la strada più breve consente di controllare meglio i propri passi e lascia più tempo per le altre domande.
Ecco, anche il nostro quesito è di questo tipo. Non ha particolari difficoltà di ragionamento, il procedimento è piuttosto chiaro. Si può arrivare alla soluzione per la via da cinque minuti, allora si applicherà il teorema di Pitagora nel modo canonico con tutti i pezzetti al loro posto. La strada da trenta secondi richiede di uscire dalla modalità "faccio il compitino" per entrare in quella "uso al meglio le competenze che mi sono costruito".
A parte queste considerazioni, entrambe le strade portano alla risposta, quindi vanno bene.
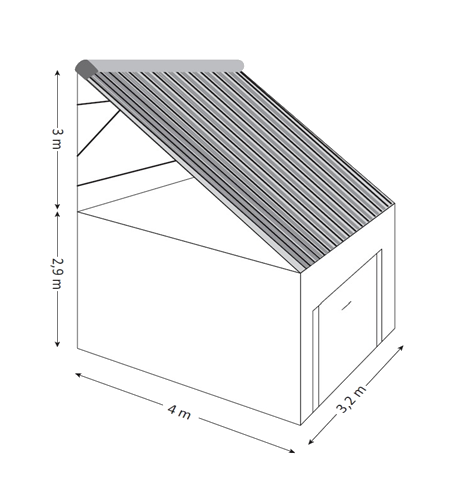
Stefano P riesce ad attivare la modalità "uso al meglio eccetera" e percorre la strada da trenta secondi:
per trovare la misura della superficie dove ci saranno i pannelli solari devo prima calcolare il lato inclinato. Misura 5m perché se i due cateti del triangolo rettangolo misurano 3m e 4m la terna pitagorica (questo è il punto chiave!) è 3m 4m e 5m. Adesso posso calcolare la misura della superficie facendo 5m X 3,2m = 16m2.Tutti gli altri hanno scelto la strada lunga.
Le risposte sono tutte simili, ne faccio una sintesi sfruttando principalmente le frasi di Edoardo O. Userò anche la figura di Nicole M, perché il colore del tetto mi piace, ecco.
Per trovare la superficie che ospita i pannelli solari:
- devo utilizzare il teorema di Pitagora per trovare l'ipotenusa del triangolo, cioè il lato della superficie dei pannelli;
- radice quadrata di 4 cm alla seconda + 3cm alla seconda= radice quadrata di 16cm quadrati + 9cm quadrati= radice di 25cm quadrati= 5cm;
- ora moltiplico la misura del lato obliquo x 3,2cm;
- 5cm x 3,2cm = 16cm quadrati.
Per la seconda B: Alberto C, Alessia P, Alice D, il solito Anonimo (sempre ammesso che sia di seconda!), Edoardo&Christian, Giorgia M, Ivan Z, Martina D, Matilde & Paolo D, Nelson R, Nicole M, Nihad K,
Per la terza B: Pietro B, Riccardo R. Naomi R fa tutto per bene ma alla fine calcola il perimetro anziché l'area.
Bene, sono riuscito anche a concludere questo post. Mi faccio i complimenti un'altra volta; chissà che aiuti la mia autostima.
Aggiungo anche i complimenti a tutti quelli che hanno risposto e a quelli che ci hanno provato con impegno.
Ringrazio la prof Giovanna per averci dato un'altra occasione per pensare e (speriamo!) imparare qualcosa in più.
Mi resta solo da dare l'appuntamento per i prossimi giochi di Sarà mica matematica. Ma non so proprio quando riuscirò a pubblicarli!
Prossimamente, può andare bene?
È una promessa.